up/down




near/far
left/right
that is
What is a group? A group has an identity, an inverse, and a binary operation (multiplication). One member of the group times another member of the group generates yet another member of the same group. This is a case where the math name is accurate: once in a group, you are always in a group.
The standard model has three continuous groups that characterize three of the four known fundamental forces of nature. The simplest group is known as U(1) and governs electromagnetism via the photon. The reason there is one photon is that the Lie algebra u(1) - note that was a small u! - has one degree of freedom. This group is called the unary group, complex numbers with a norm of 1. The members of this group commute, so it does not matter the order things are written in. Quaternions have this property only when all point in the same or opposite directions, which is the case for when using one quaternion times itself.
The continuous group SU(2) rules the weak force, the stuff driving radioactive decay. Mathematically this is call unitary quaternions, quaternions with a norm of 1. The Lie algebra used to generate this group has three degrees of freedom. That is why the weak force is mediated by three particles, the W+, W-, and the Z.
The group SU(3) is for the strong force whose residual interactions keep nuclei together. Its Lie algebra has eight members, and there are eight gluons.
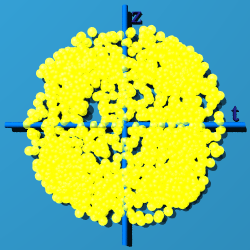
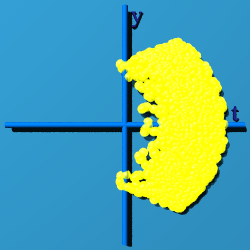
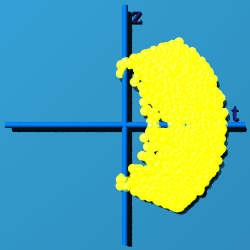
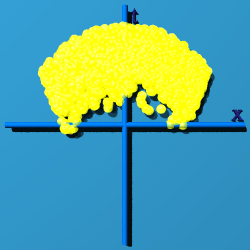
Start with a simple picture, layer pictures together, and we will be able to see what the standard model of particle physics looks like.
up/down |
||

|
 |
 |
 |
 |
 |
near/far |
left/right |
that is |
up/down |
||
|
 |
 |
 |
 |
 |
near/far |
left/right |
that is |
up/down |
||
|
 |
 |
 |
 |
 |
near/far |
left/right |
that is |
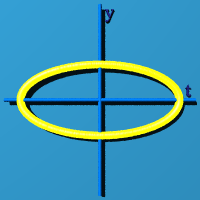
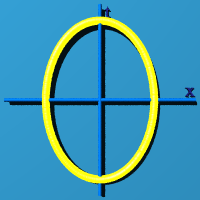
Another way to represent S2 is to set x=0. Then you have an edge view of an expanding circle.
up/down |
||
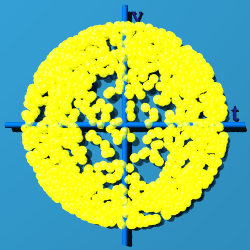
|
 |
 |
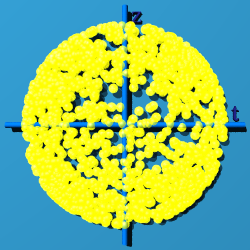 |
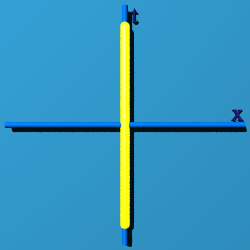 |
 |
near/far |
left/right |
that is |
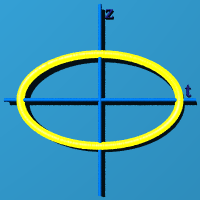
If z=0, at least you can see the "circleness"
up/down |
||
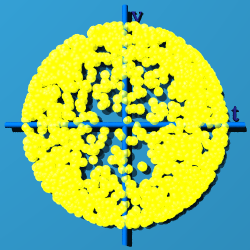
|
 |
 |
 |
 |
 |
near/far |
left/right |
that is |
up/down |
||
|
 |
 |
 |
 |
 |
near/far |
left/right |
that is |
up/down |
||
|
 |
 |
 |
 |
 |
near/far |
left/right |
that is |
up/down |
||
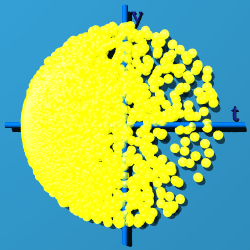
|
 |
 |
 |
 |
 |
near/far |
left/right |
that is |
up/down |
||

|
 |
 |
 |
 |
 |
near/far |
left/right |
that is |
It would be great to include gravity, which is all about how measurements change as one moves around a differentiable 4D manifold. Include the metric as part of the calculation of a quaternion product.
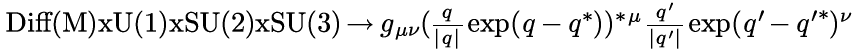
What happens if q=q'? That is shown below:
up/down |
||
|
 |
 |
 |
 |
 |
near/far |
left/right |
that is |
OK, but what does that mean? Here is my take. Observers sit at here-now in spacetime, or numerically at (0, 0, 0, 0). An observer sees something out there, and tries to characterize the "thingie". The basic bit of information it can classify is an event. Whatever set of events is collected, they are all tied up in describing this one thingie out there. Every event contributes to the description of the thingie, and so makes a group. The multiplicative identity of a quaternion, (1, 0, 0, 0) is a way to represent the thingie. Almost none of the events map to (1, 0, 0, 0). The events are scattered all around spacetime. U(1)xSU(2)xSU(3) is the way to cow-rope all the events and bring them home, while remaining part of the same group, the one thing being observed.
Home
Page | Quaternion Physics |
Pop
Science
Java
| The Bike | Lindy
Hop | Contact Doug
Copyright © 2007, doug <sweetser@TheWorld.com> All rights reserved worldwide