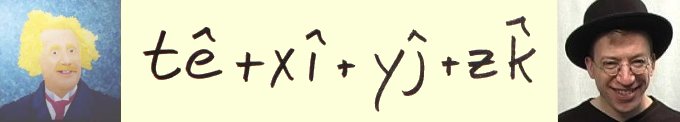

A brief history of quaternions
Multiplying quaternions the easy way
Scalars, vectors, tensors and all that
Quaternion analysis (pdf, related video: "Why Quantum Mechanics is Weird")
Where quaternions fit in math, adapted from Max Tegmark, 1998.
- written in Java 1.0, so is broken :-(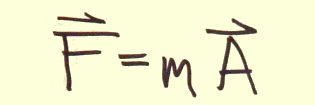
F = m a, in an inertial frame, in polar coordinates, and in a rotating reference frame
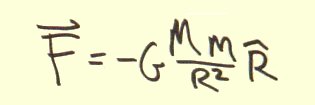
I think it is reasonable to believe I have found a way to unify gravity with the forces of electromagnetism, the weak and strong forces in a way that can been quantized. Only unloved math tools are used. The problem is a puzzle to be solved, not a math problem so difficult only a few folks at the Institute for Advanced Study to understand. At the core is the action, shown here, which requires both quaternions and hypercomplex multiplication (indicated by the box-times), keeping only the scalar. My paper is here ( Mathematica notebook, html, or pdf)
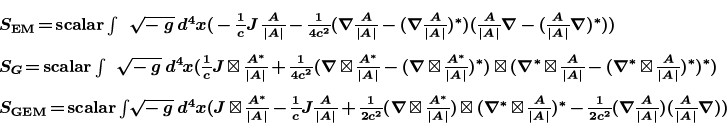
Geometry + 4-Potentials = Unified Filed Theory, 2007 April APS talk available as html or YouTube video.
Unifying Gravity and EM, a Riddle You Can Solve (pdf), 9th Eastern Gravity Meeting, 2006.
Why a Rank 1 Unified Field Theory is Compelling and Its Background Mathematical Structure (pdf), 8th Eastern Gravity Meeting, 2005.
Unifying Gravity and EM by Generalizing EM (pdf), 7th Eastern Gravity Meeting, 2004.
Unifying gravity and EM by analogies with EM, MIT IAP course, Jan. 2003.
Realizing Einstein's Dreams: Unifying Gravity and Light, and Why Quantum Mechanics is Weird (pdf), Joint APS/AAPT meeting, Spring 2005.
4-potential Equations for Gravity and Electromagnetism (pdf), Joint APS/AAPT meeting, Fall, 2003.
The Cosmological Consequences of the Product Rule (pdf), Joint APS/AAPT meeting, Spring, 2004. A Universe with zero dark matter is good :-)
Picture Stories of Events in Spactime (pdf), Do While Studios, Spring 2000. The relationship between Special and General relativity using quaternions.
A family of variations on the Maxwell action using quaternions and hypercomplex numbers contains the symmetries of the standard model and a testable gravity theory (pdf)
(my current best effort, version 20091119)
OLDER EFFORTS... an approaching using standard tensors and differential geometry
Deducing a Unified Field Theory from Electromagnetism (pdf).
Unifying Gravity and EM by analogies to EM (pdf) (v 4.4, 13 pages).
Geometry + 4-Potential = Unified Field Theory, submission for the 2007 Essays on Gravitation, sponsored by the Gravity Research foundation (pdf)
An approach using quaternions.
Einstein's Vision I: Classical unification of gravity and electromagnetism using Riemannian quaternions (pdf)
Einstein's Vision II: Unified force with constant velocity profiles (pdf).
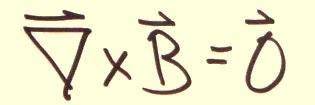
The Maxwell equations in the light gauge: QED?
The stress-energy-momentum 2-tensor of the electromagnetic field
Paper: Maxwell's vision: electromagnetism with Hamilton's quaternions (pdf), Second Meeting on Quaternionic Structures in Mathematics and Physics, Rome, 1999.
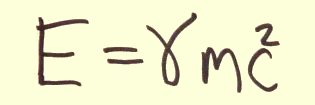
Doing the work of the Lorentz group with rotations and dilations
An alternative algebra for boosts
Index and links to solved problems
PS 1: Kinematic effects of relativity
PS 3: The Lorentz transformation and the addition of velocities
PS 4: The Doppler effect, 4-vector invariants, and the twin paradox

For a fee: Books, Buttons, Turquoise Einstien T-shirts, and No Stinking Higgs t-shirts
For free: Doing Physics with Quaternions (much of this site, 156 pages), Lectures on Dynamic Graphs and Unified Field Theory (75 pages).




A few good papers:
Home Page | Quaternion Physics | Old index page | Pop Science
Java | The Bike | Lindy Hop | Contact Doug
Copyright © 1997, doug <sweetser@alum.mit.edu> All rights reserved worldwide.