sweetser@alum.mit.edu

39 Drummer Road, Acton, MA 01720

 Abstract 

Logic will dictate the equations for gravity based on those for electromagnetism. The classical action of electromagnetism is broadened to include a symmetric tensor and a charge where like charges attract. Since the action breaks U(1) symmetry for massive particles, the Higgs mechanism is unnecessary. The 4D wave equation contains the classical static laws of Gauss and Newton’s law of gravity within the context of a tensor equation consistent with special relativity. It is shown how the Rosen metric is a solution to the field equations, and thus is passes weak field tests of gravity to first-order Parameterized Post-Newtonian (PPN) accuracy, and is distinguishable from general relativity at second-order PPN accuracy. Spin 1 and spin 2 fields are required to have like electric charges repel and like mass charges attract. The linear field equations should be quantizable using standard techniques.

DRAFT: Deducing a Unified Field Theory from Electromagnetism (pdf)

1  Introduction

Classical electromagnetic theory has been remarkably robust to modern innovations. It was the inspiration for special relativity and did not need alteration. As quantum mechanics evolved, the field equations remained the same. One technical change was in the action, a gauge had to be chosen. The advent of general relativity did not alter electromagnetism. Instead, general relativity provided the background metric needed by electromagnetism. The U(1) symmetry of electromagnetism served as the starting point for the formation of the standard model, which unifies electromagnetism, the weak, and the strong forces. A problem with this picture is the separation of gravity from the forces of the standard model. In this paper, I use electromagnetic theory to deduce the laws that govern gravity.

2  The Action

The classical action for electromagnetism has three terms, a contraction of the irreducible antisymmetric field strength tensor and a coupling of electric charge with the potential, and an inertia term. To be logically complete, Nature must also exploit a contraction of an irreducible symmetric field strength tensor. The symmetric field will be associated with a different charge current that couples with the potential because the tensor is irreducible and thus an independent fundamental force. This new force must be long range like electromagnetism. The only such force is gravity.

Like charges repel in the electromagnetic action for several reasons. First, the signs of the charge coupling and the field strength tensor contraction are the same. The field equations that arise from varying the action with respect to the potential keeping the velocity fixed will have like charges repel.[cite{landau1975}] Second, the signs of the charge coupling term and the inertia term are the same. Varying the action with respect to velocity keeping the potential fixed generates the Lorentz force where like charges repel. Third, the field strength tensor is antisymmetric, so it must be represented by an odd spin particle, the spin 1 photon. For gravity, like charges attract. The coupling term must have the sign opposite to the field strength contraction and inertia terms so both the field and force equations will have like charges attract. A traceless symmetric rank 2 tensor can be represented by a spin 2 particle that travels at the speed of light like the photon, so the particle matches the description of a graviton. Based on these deductions, the action for gravity and electromagnetism (GEM) can be written:

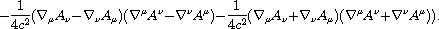
The current coupling term appears more complex than one might anticipate. The reason is that this current coupling must represent both a spin 1 and a spin 2 current-current interaction. One is free to choose the orientation of the theoretical 4-potential with the actual 4-current, derived from the 4-potential via a Fourier transformation. Where there is freedom, there is a physics message. In this case, we have freedom with the phase for the current-current interaction. The part of the potential that is tranverse to the current can be separated from that which is parallel. The phase of the current-current interaction for the transverse potential-current has the symmetry of a spin 1 field, as is needed to have like charges repel. Rotating the longitudinal current around the parallel axis accomplishes two things. First, the sign of the coupling term must change to conserver the correct signs of the contraction of the current density with the potential. Second, the phase of the current-current interaction for the rotated longitudinal potential-current has the symmetry of a spin 2 field. A even spin field is required for like charges to attract.

The current density is made of difference between the electric current density and the mass current density, using the square root of Newton’s gravitational constant with the mass current density so the units are identical. Electric charge is only known to ten significant digits, while for fundamental particles, the mass in electrical units can be more than thirteen orders of magnitude smaller. At this time, I have no notion why there is this large difference, but it justifies the practice of working on problems in electromagnetism separately from gravity.

The deep insight into gravity provided by general relativity is that the geometry of spacetime is not presumed. In special relativity, the metric must be constant, the same for all inertial observers. In general relativity, the metric can vary depending on where the observer is in spacetime: closer to a mass source will have more spacetime curvature. The Riemann curvature tensor is a rank 4 tensor that contains second order derivatives of the metric. The Hilbert action has the Ricci scalar, a contraction of the Riemann curvature tensor. By varying the Hilbert action with respect to the metric tensor, the geometry of spacetime can change as dictated by the Einstein field equations.

Electromagnetism works no matter what the metric happens to be. The antisymetric tensor cannot characterize how the symmetric metric tensor changes, so the possibly dynamic metric must be supplied as part of the background mathematical structure. By including a symmetric field strength tensor in the GEM action, it becomes possible for the action to account for the changes in metric tensor, and thus remove the metric from the background structure. The idea is not to treat the metric as an active field, but instead to use a symmetry of the action to provide a constraint on a metric that varies in spacetime.

The way gravity in the GEM action works mathematically is different from general relativity. The Hilbert action requires only one field, the metric field, to be varied in the action to generate the Einstein field equations. The GEM action does not treat the metric as a field. Instead there is a diffeomorphism symmetry of the action that allows one to chose how much of a covariant derivative is due to a dynamic potential or a dynamic metric. Where there is a symmetry, there is a conserved charge. Since the symmetry involves the metric, the charge must be mass. Energy and momentum also arise from a symmetry of the action. Since mass is the square of the energy minus the square of the momentum, it is logically consistent that energy, momentum, and mass all can be viewed as different symmetries of the same action.

The action has U(1) symmetry for massless particles. Mass charge breaks U(1) symmetry. This is an attractive feature because it means the Higgs mechanism for introducing mass into the standard model is unnecessary. The GEM proposal predicts the Higgs boson will not be found in particle field experiments such as the Large Hadron Collider. The trace of the symmetric field strength tensor is a scalar field which plays the role of the Higgs.

3  Field Equations and Solutions

The field equations can be determined in the usual way by fixing the metric tensor up to a diffeomorphism and then varying the action with respect to the potential:

This 4D wave equation has the ability to describe 4 modes of emission of particles that travel at the speed of light. The two transverse modes are electromagnetism. That leaves the scalar and longitudinal modes for the graviton.

It is critical to note in eq. 4D_wave_eq the scalar D’Alembertian operator is not acting alone on the potential. Instead, two covariant derivatives are applied to the potential. A covariant derivative contains both the normal derivative and the connection. The complete wave equation is composed of the D’Alembertian operator acting on the potential, the divergence of the connection, the connection of the first derivative of the potential, and the connection of the connection. Spacetime is nearly flat if one excludes regions near black holes, so the connection of the connection term can be ignored. The divergence of the connection contains second derivatives of the metric, so in principle could provide an equation that must be solved to determine a smoothly changing metric.

Because eq. 4D_wave_eq is valid up to a diffeomorphism of the metric, the equation cannot be solved until that degree of freedom is eliminated. In this paper, I will work with metric compatible, torsion-free connections as is done in general relativity. If one chooses to work with a flat Minkowski metric in Euclidean spacetime, the connection will be zero everywhere. For a static point charge, the first field equation is a sum of the static form of Gauss’ law of electric charge and Newton’s law of gravity:

The repulsive force of like electric charges is decreased by mass attraction. This field equation can account for all classical effects of Gauss’ and Newton’s law because it is identical to their superposition. There are two articles in the literature that assert without proof that one cannot form vector field equations where like charges attract.[cite{gupta1957}][cite{thirring1961}] Perhaps there was an aversion to putting a negative sign in front of the mass. What matters are the relative signs, that the mass charge density has the same sign as the Laplacian operator in eq. Gen_Gauss_law_static.

A flaw of Newton’s law of gravity is that it requires changes in the charge density to propagate instantaneously, which is not consistent with special relativity. One road to Einstein’s field equations is to make Newton’s law respect special relativity.[cite{weinberg1964}] Here is the dynamic form of the equation (I will refer to it as “General Gauss’s law” out of respect for both the Swiss master and Chinese food):

The waves for gravity and light both propagate at the speed of light. This equation transforms as the first term of a 4-vector equation and so is manifestly covariant under a Lorentz transformation.

The gauge choice - how one measures things - for the GEM action concerns how to measure a covariant derivative: how much should be due to the standard derivative versus how much is due to the connection, the changes in the metric? In the preceding paragraphs, a choice was made that everything was due to the standard derivative of the potential. This time I choose to allow all of the change be due to the connection, nothing due to the standard derivative of the potential. The first field equation under this gauge choice for a static charge is:

A metric must be found whose connection solves this first-order partial differential equation. This might appear like a difficult task since the connection has three derivatives of the metric. Yet one of the derivatives is zero because the charges are static. If the metric were diagonal, another of the derivatives would be zero. The metric must reduce to the Minkowski metric as the charges go to zero. The exponential metric below provides a solution with these properties to eq. ChristoffelDivergence:

For an electrically neutral source, the metric becomes the Rosen metric.[cite{rosen1973}] That metric is not a solution to the Einstein field equations, but has been studied in the literature because it is consistent with experimental tests of gravity to first order parameterized post-Newtonian (PPN) accuracy. At second order PPN accuracy, eq. exponential_metric predicts 0.7μmicroarcseconds more bending of star light by the Sun.[cite{epstein1980}] An experiment such as LATOR, could confirm or reject this proposal on purely experimental grounds.[cite{turyshev-2006-}]

The bimetric theory of Rosen is not consistent with strong field tests of gravity. The fixed background metric can store momentum, allowing for bipolar modes of emission of gravity waves which are ruled out by observations of binary pulsars. The GEM action does not have an additional field to store momentum. For an isolated source, the lowest mode of emission that conserves momentum will be the quadrapole mode, consistent with observation.

4  Quantization

The 4D wave equation, eq. 4D_wave_eq, has already been quantized by Gupta and Bleuler.[cite{gupta1950}][cite{bleuler1950}] They were quantizing the field only to do the work of electromagnetism in a manifestly covariant way. The transverse modes of emission do the work of electromagnetism. The scalar mode of a spin 1 field caused a serious technical problem: it suggested negative probability states. To solve this issue, a supplementary condition was imposed to eliminate both the scalar and longitudinal modes.

There are two independent ways to spot the spin 1 field in the classical electrodynamic Lagrangian. The first is by looking at the anti-symmetric, rank two field strength 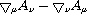tensor, . If the indexes are swapped, then all the signs flip, the sign of an odd spin tensor.

The second approach considers current-current interactions of the charge coupling term, - J^μA_μ. One can take the Fourier transformation of the 4-potential and write it as a current density in the momentum representation, - (1/k²)J′J_μ. If one constrains the current to move along the z axis, conservation of electric charge can be used to eliminate the current density. The current-current interaction is thus:

The current along the z axis is real. The currents along x and y are for the two independent polarizations of virtual photons needed for relativistic corrections. What is the symmetry of these virtual photons? Form the product of these two virtual currents (using quaternion algebra):

The phase part of this product (the z component) will require a 2π rotation to return its original location, a defining characteristic of a spin 1 field.

The GEM action has the antisymmetric field strength tensor, and this kind of current-current interaction. On a quantum level, the work of photons can be done.

The GEM action also has a spin 2 field. There is a symmetric, rank 2 field strength tensor, 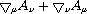. If the indexes are swapped, then all the signs stay the same, the sign of an even spin tensor. Since the tensor has indexes, it cannot be a scalar field. A spin 0 field can be formed by taking the trace of the symmetric field strength tensor, a Lorentz invariant quantity. If the trace is zero, then the particle can travel at the speed of light c. If the trace is not zero, then the scalar field formed will break gauge symmetry. In other words, a scalar inertial mass field breaks gauge symmetry. The Higgs mechanism is not necessary.

The analysis of the current-current density proceeds along lines similar to the case for electromagnetism. There is a difference for calculating the product of two currents. The real current is the one along z, yet the current along z does not appear in Eq. eq:jxy. Although the reader may realize the currents along x and y in Eq. eq:coupling are virtual, it would be preferable to enforce that they are zero. Working with pairs of currents with xz and yz, it may be possible to do both. The conjugate used in Eq. eq:jxy is not the only anti-involutive automorphism. There is also a conjugate that flip all the signs but the first term of the 3-vector (referred here as the first conjugate, or symbolically as (iqi)*≡^*1). One can also construct the second conjugate to keep the sign of the y current positive while flipping all others. Form products using these operators:

These products have the character of spin 2 because the two parts add together, allowing a return after only a π rotation. If the three product currents are added together, Eq eq:jxy, Eq eq:jxz, and Eq eq:jyz, the result has the real current along the z axis, and phases for spin 1 and spin 2 polarization modes. The four modes account for the four degrees of freedom in the 4-current. The scalar and longitudinal modes of emission will do the work of gravity. General relativity predicts transverse modes of emission for gravity waves. Should a gravitational wave detection experiment succeed, the polarization of the gravity wave will serve as an experimental test of this proposal.

There is a strong belief that field equations for gravity must be nonlinear. To be more precise, this means that gravity fields gravitate. The same is not true for electromagnetism: the electromagnetic field cannot be a source of charge. There are thought experiments to support the notion that gravity must be nonlinear. An example from a review paper on general relativity had two boxes with six neutral particles in each. Imagine that the rest mass of one particle were to be converted entirely into the kinetic energy of the other five. Would the first box be able to tell any difference in energy density and spacetime curvature between the two? If the answer is no, gravity must be governed by a nonlinear field equation.

Repeat the thought experiment, but this time make all the particles positively charged. Now the thought experiment cannot be done because it would involve destroying an electric charge. There are solid theoretical and experimental tests demonstrating that electric charge cannot be destroyed. Because the thought experiment cannot be done, the conclusion is not supported.

5  A New Implementation

The experimental tests of the equivalence principle indicate that gravity must be a metric theory. This paper questions how to implement a metric theory. General relativity takes a direct approach: start with the Riemann curvature tensor that characterizes how a metric changes, and put its contraction the Ricci scalar into the action. This paper uses the symmetry found in the definition of a covariant derivative to allow spacetime geometry to change based on what mass is in that spacetime. It is the flexibility of the spacetime geometry that indicates the approach can be characterized as a metric theory.

There is a well-known thought experiment of a man in a closed box who would be unable to tell if he was in a smoothly accelerating rocket ship or the box was sitting on the surface of a planet (ignoring tidal effects). For the box on the planet, general relativity would be able to generate a metric equation that in a limit process, would become a potential theory. For the GEM approach, one could choose a dynamic metric which would be equivalent to first order PPN accuracy to the metric from general relativity, or with the practical power of a diffeomorphism, choose to work in a flat spacetime and have a 4-potential completely characterize the gravitational field (see figure 1). A scalar potential like Newton’s law of gravity is inadequate because there is only one parameter, so it gets the answer to light bending around the Sun half right. With four parameters, a 4-potential can describe the way measurements of both time and space are bent by a 4-momentum current density.

The GEM action is to a surprising degree exactly what Einstein searched for over the last half of his life.[cite{pais1982}] He tried an impressive range of ideas, from five dimensional Kaluza-Klein variations, to asymmetric Riemann curvature tensors, all to no avail. The radical approach used here is to abandon the Riemann curvature tensor, and work only with the building blocks of the curvature tensor, the connection as found in a covariant derivative. The 4D wave equation in this paper was called beautiful by Feynman in his lecture series.[cite{feynman1964}, Volume II, 18-11] Elegance governs the heavens.

References

[1]	K. Bleuler. Helv. Phys. Acta, 23:567, 1950.
[2]	R. Epstein and I. I. Shapiro. Post-post-newtonian deflection of light by the sun. Phys. Rev. D, 22(12):2947–2949, 1980.
[3]	R. P. Feynman, R. B. Leighton, and M. Sands. The Feynman Lectures on Physics. Addison-Wesley, 1964.
[4]	S. N. Gupta. Theory of longitudinal photons in quantum electrodynamics. Proc. Phys. Soc., 63:681–691, 1950.
[5]	S. N. Gupta. Einstein’s and other theories of gravitation. Rev. Mod. Phys., 29:337–350, 1957.
[6]	L. D. Landau and E. M. Lifshitz. The Classical Theory of Fields. Pergamon Press, 1975.
[7]	A. Pais. ’Subtle is the Lord...’: The science and the life of Albert Einstein. Clarendon Press, 1982.
[8]	N. Rosen. A bi-metric theory of gravitation. General Relativity Gravitation, 4(6):435–447, 1973.
[9]	W. E. Thirring. An alternative approach to the theory of gravitation. Ann. Phys. (U. S. A.), 16:96–117, 1961.
[10]	S. G. Turyshev, M. Shao, and K. L. Nordtvedt. Science, technology and mission design for the laser astrometric test of relativity, 2006.
[11]	S. Weinberg. Derivation of gauge invariance and the equivalence principle from lorentz invariance of the s-matrix. Phys. Let., (9):357–359, 1964.