If a sequence of reals converges, then either it converges to a rational number or it doesn't. If it converges to a rational, we're done. If it doesn't, then the sequence divides the rationals into two sets: those above the tail of the sequence and those below the tail.
As the tail of the sequence becomes arbitrarily narrow—that's what it means to converge—every rational number eventually ends up in one set or the other et voila we have a Dedekind cut, A.K.A. an irrational number, which is a real number.
QED
Anthony is an anteater. He eats ants—off the ground.

For this purpose, he has a long, thin tongue, covered in sticky saliva. When Anthony sees an ant, he flicks his tongue out to the ant. The ant sticks to his tongue, and then Anthony slurps his tongue back into his mouth and eats the ant. Yum!
Rachael is a rateater. She eats rationals—off the number line.
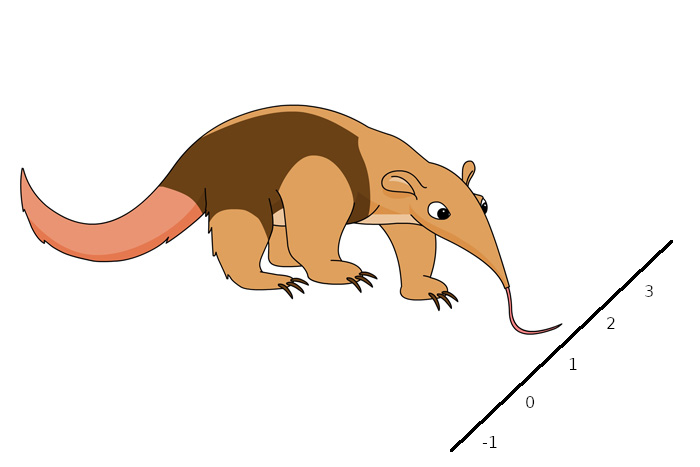
Like Anthony, Rachael has a long, thin tongue. When Rachael sees a rational, she flicks her tongue out toward the number line. As her tongue approaches the number line, the tip gets longer and thinner, and longer and thinner, until—just as it reaches the number line—the tip narrows to a single point. The rational sticks to that point. Then Rachael slurps her tongue back into her mouth and eats the rational.
But sometimes Rachael's aim is not so good. She flicks her tongue out to the number line, but the tip lands on a spot where there is no rational. When this happens, I tell Rachael not to be sad. I tell her that what she has gotten then is an irrational number.
But Rachael will not be consoled. She says that no, really, there is nothing there, and she is still hungry.
I think Rachael is a finitist.