POTENTIAL FOR POSITIONAL VARIATION IN FLOW CALORIMETRIC SYSTEMS



Mitchell Swartz
JET TECHNOLOGY.
rev. February 15, 1996



ABSTRACT
Although many aspects of calorimeters have been discussed, including issues of potential problems with the thermometry [i.e. thermocouples, thermistors and thermometers, including electrical grounding and crosstalk, thermal mixing and sensor positioning problems], the potential impact of positional effects of the flow calorimetry has not been mentioned. The positional orientation refers to the direction of the flow, and not to the orientation of any temperature probes therein. Despite the reported advantages for flow calorimetry in detecting enthalpy from putative fusion reactions, these studies theoretically suggest that there may be effects from positional variation in the calorimetry of such flow systems. Rather than 'ease of calibration' usually touted for such systems, it is suggested that calibration may be more complicated for vertical flow calorimetric systems. In the absence of additional calibration, it may be critical to keep semiquantitative calorimeters horizontal under some conditions.

INTRODUCTION
One recent series of reports using vertical flow calorimetry1,2,3,4 involves the CETI microspheres, reported to use a few percentage of the metal of other systems. The microspheres have multilayer metallic coats and are used as a distributed electrode bed. The cell is 10 cm long, 2.5 cm in diameter, and contains 1 to 40 ml of beads. Electrolyte percolates through, removing the heat, and exits from the top. The flow causes a temperature gradient. The observed delta-T, between the top and bottom, is in the range of 1.5 to 20C [flow rates to 1.0-1.5 liters per minute, with the water circulated by a magnetic impeller pump, total power consumption ~85 watts]. At the ICCF5, the CETI cell was reported to have an input of 0.14 watts and a peak excess of 2.5 watts, a ratio of 1:18. At SOFE '95, the CETI cell had 0.06 watts input and 5 watts peak output, a ratio of 1:83. At Power-Gen, the ratio reportedly ranged from 1:1000 to 1:4000.

There have been several complaints suggested regarding the CETI demonstrations concerning recombination, flow measurement, and inadequate heat ejection3. Assuming the thermometry is correct, it is instructive to closely examine the calorimetry using a computer model representing heat and mass transfer. The equation used to derive the output, and therefore the presence of any excess heat involves the flow, the specific heat of the water, and the temperature differential. Although this equation may be dimensionally correct, it may not be valid for low flow rates in certain cases discussed below. The role of the Bernard instability5 has not been previously mentioned, even though it may have inadvertently impacted the calorimetry4.

EXAMINATION OF MODEL
The following describes the result of a quasi-one-dimensional (Q1D) analysis which further examined the impact of the flow orientation with respect to the gravitational field, during flow calorimetry. The model generated to test the hypothesis examined convection, conduction, and gravity-thermal instabilities. Figures 1 through 4 show four groups of curves which show the time-varying distribution of temperature in such a quasi-one-dimensional model.




































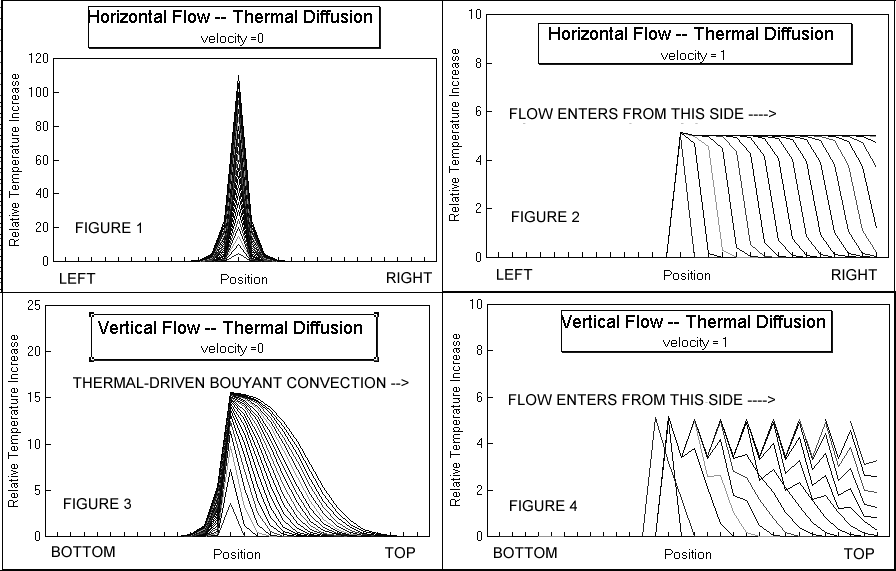
The four groups of curves represent horizontal and vertical flow calorimetry, both with and without convection. In each graph, the spatial distribution of heat (in one dimension) is represented as a single curve. There is one curve for each point in time. There is heat input from a single point source -- at midposition along the x-axis -- during the entire time subtended by each series of curves. The earliest curves, in each group, are those closest to the x-axis where the heat arise out of the central point source. Thus the dynamics can be followed from the graphs generated from the model.

After the heat enters at the midposition along the x-axis, it can be redistributed by thermal conduction, by convection, and by redistribution secondary to the changes in specific gravity resulting from the temperature change (as with the Bernard instability). Radiative loss is not considered in this simplified model. The first group of curves is in figure 1, which is labeled "Horizontal Flow -- Thermal Diffusion" to indicate that the flow is horizontal to the Earth's surface and that thermal diffusion is included. Figure 1 shows both the midline exogenous heat component and a slow thermal diffusion away from the point-source of heat. The velocity is zero; that is, there is no convection. The second group of curves, figure 2, show the impact of convection upon the spatial distribution of heat. This figure shows how the redistribution of heat is used in typical flow calorimetry to generate a temperature gradient, from a sampling of which a calculation is made to determine the output heat (energy). The next two groups of curves, figures 3 and 4, labeled "VERTICAL FLOW" represent the output from a vertical system, both with and without the addition of upward thermal-driven convection. The extrema along the x-axis away from the point source of heat input, previously 'right' and 'left' in figures 1 and 2, are now 'top' and 'bottom' in figures 3 and 4.

Upon examination of the curves on the lower left, gravity is observed to now play a role in the distribution of the warmed water. It is saliently obvious that because of thermal-driven bouyancy which also leads to the Bernard instability -- where hot water rises due to its lower specific gravity -- the curves in figure 3 do shift in position away from the symmetry exhibited by horizontal flow calorimetric systems even in the absence of convection (compare to figure 1). There may be, for such conditions, an apparent "signal" for zero flow because of the thermal instability, which simulates the effect of flow (the group of curves in figure 3; compare to the group of curves in figure 2). The addition of convection produces a contribution to the heat shift in the vertical flow system (figure 4), quite similar to that which it does for horizontal systems (figure 2).

One observation from the model is that the boundary condition for zero to negligible flow conditions is different for the horizontal and vertical flow calorimetric systems. It is important to consider that generally, quoted efficiencies of energy generated from putative over unity devices are calculated assuming the standard equation is always correct. Another salient observation resulting from this theoretical Q1D study is that simple equations which apply for horizontal calorimetric systems may not be strictly applicable for vertical flow calorimetric systems for low flow conditions. But which?

We now define hB as the ratio of heat transported by the buoyant forces to the heat transported by solution convection.

heat transported by buoyant forces
hB = --------------------------------------
heat transferred by solution convection


This Q1D model of heat and mass transfer has indicated that what is generally correct for horizontal calorimetric systems, may not be correct for vertical systems, when the non-dimensional number (=hB) is significantly greater than zero. Any apparent amplification of the 'excess heat' (if any, and there does appear to be some) would be greatest at the low flow levels. Increased flow makes the positional error less important. As a corollary, any false excess heat, or excess heat magnification, should also reduce with increased flow.

SUMMARY
In summary, thermometry may not be the only rate limiting factor for obtaining high-quality information from flow calorimeters if the non-dimensional number, hB {defined as the ratio of heat transfer by bouyancy to the heat transfer by convection} is greater than zero. hB , in a real system where viscosity, turbulence, and other parameters play a role, depends upon other non-dimensional factors including the Archimides non-dimensional number which is the ratio of the buoyant force to the viscous force, and possibly the Rayleigh non-dimensional number, which is the ratio of gravity to thermal conductivity. Studies are underway to explore this. It is also proposed that a simple test of the theory would be to build a rotatable flow cell with a resistive heat element, perhaps mounted on a goniometer for any system to check sensitivity. This hypothesis, and Q1D model of heat and mass transfer, do not imply that such systems do not exhibit 'excess heat'. But rather that any such reported 'excess heat' parameters may be inflated, if the information was indeed collected with a vertical flow calorimetric system, in the absence of confirmatory calibrations under low to moderate flow conditions where the non-dimensional number (hB) is not trivial.


REFERENCES


The author is most grateful to Gayle Verner, Hal Fox, Horace Heffner, Mark Hugo, Jed Rothwell, Barry Merriman and Michael Schaeffer and Profs. Louis Smullin and Keith Johnson of MIT and the staff of JET Technology and Fusion Information Center for helpful comments and assistance during the development of this model and the preparation of this manuscript.


If you have a comment, or suggestion, or criticism, please do not be reticent to share your thought. Send an e-mail message, and please label the subject as "positional"

-----> click here to generate an e-mail form




(c) JET Technology, USA