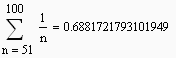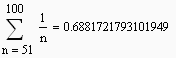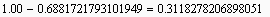There are 100! ways to fill the 100 boxes
The probability of a cycle of length n, n>50, is (The number of ways of arranging the boxes in a cycle of n)/100!
There are 100!/n!(100-n)! ways of selecting the n boxes which make up a cycle of length n.
For each such cycle there are (n-1)! ways of arranging those particular n boxes into a cycle
For each arrangement there are (100-n)! ways of filling the other (100-n) boxes
The number of ways of arranging the boxes in a cycle of n is the product of these three numbers. That product simplifies to 100!/n. So the probability of a cycle of length n is 1/n.
There can be at most one cycle of length greater than 50, thus there's no overlap of events. The probability of a cycle of length greater than 50 is therefore
Hence the prisoners have a probability of
of survival, which is better than the chances of getting a pardon from Gov. G.W. Bush.
The Prisoners Problem
An excellent strategy

Eva's Home Page 

Jean-Claude Chetrit heard this problem and strategy at a conference 
and shared it with the Brooklyn Go Club email list little by little in a 
way that promoted enjoyable back and forth. Eva Casey worked out the probability 
to her own satisfaction and saved it to html format using Mathcad.
Send feedback to eva@theworld.com
This page has been accessed access odometer display times since June 12, 2007 
 Last Revised Feb 7, 2009