Douglas B Sweetser@alum.mit.edu
Create one mathematical structure for gravity and electromagnetism that can be quantized.
The difference between gravity and electromagnetism is the oldest core problem facing physics, going back to the first studies of electromagnetism in the seventeenth century. The best minds on the planet are trying to merge the Riemannian geometry of general relativity with the quantum field theory of the standard model. Three lines of attack are string theory in ten or eleven dimensions, loop quantum gravity, and non-commutative geometry. These approaches are technically challenging.
Gravity was the first inverse square law, discovered by Isaac Newton. After twenty years of effort, he was able to show that inside a hollow massive shell, the gravitational field would be zero. Ben Franklin, in his studies of electricity, demonstrated a similar property for an electrically charged hollow sphere. Joseph Priestly realized this meant that the electrostatic force was governed by an inverse square law just like gravity. Coulomb gets credit for the electrostatic force law modeled on Newton's law of gravity.
Hundreds of years later, Einstein started from the tensor formalism of electromagnetism on the road to general relativity. Instead of an antisymmetric field strength tensor, Einstein used a symmetric tensor. There is a precedence for transforming mathematical structures between gravity and electromagnetism.
The process of transforming mathematical structures from electromagnetism to gravity will be continued. Specifically, the gravitational analog to the Lorentz force will be written, as well as the gravitational analog to the classic electromagnetic Lagrangian.
![]()
Lagrangian = mass - charge * velocity contracted with the potential - field strength tensor contracted with self.
![]()
![]()
![]()
![]()
For locally covariant coordinates, ![]()
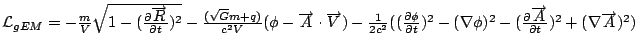
![]()
![]()
![]()
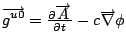
![]()
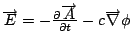
![]()
Source equations: Gauss' law and a dynamic g (or Newton's field equations under certain conditions).
![]()
![]()
One can recover Newton's field equation,
![]() ,
in isolation if:
,
in isolation if:
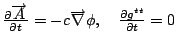
Gauss' law,
![]() ,
can also be recover if:
,
can also be recover if:
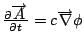
Ampere's law.
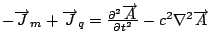
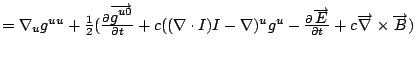
![]()
![]()
![]()
![]()
![]()
![]()
![]()
2 traverse (photons for EM),
1 scalar (gravitons for g),
1 longitudinal (gravitons for g).
Phrase ``scalar photon" is non-sense because photons transform like vectors.
When gravitational waves are detected, this proposal predicts they will have scalar (timelike) polarity or longitudinal polarity, not transverse polarity as predicted by general relativity.
The standard model does not obviously deal with curved spacetime. The unitary aspects of the symmetries U(1), SU(2), and SU(3) will be condensed with the 4-vectors and metric. Start with the standard model Lagrangian:
![]()
where
![]()
![]() with a 4-vector is to use a metric. Since it is complex-valued, use
the conjugate like so:
with a 4-vector is to use a metric. Since it is complex-valued, use
the conjugate like so:
![]()
The parity operator flips the sign of the spatial part of a 4-vector.
![]()
Normalize the potential.
![]()
From this, it can be concluded that the normalized 4-vector is an element of the symmetry group U(1) if the multiplication operator is the metric combined with the parity and conjugate operators. The same logic applies to the 4-vector potentials for the weak and the strong forces which happen to have internal symmetries.
In curved spacetime,
![]()
Mass breaks U(1), SU(2), and SU(3) symmetry, but does so in a precise
way (meaning you can calculate what
![]() should equal). There is no need for the Higgs mechanism to give particles
mass while preserving U(1)xSU(2)xSU(3) symmetry, so this proposal
predicts no Higgs particle will be found.
should equal). There is no need for the Higgs mechanism to give particles
mass while preserving U(1)xSU(2)xSU(3) symmetry, so this proposal
predicts no Higgs particle will be found.
![]()
Force = charge * velocity * field strength tensor.
![]()
Note: the gravitational force and the electromagnetic force behave differently under charge inversion, if mass goes to negative m or electric charge goes to negative q.
fbox
![]()
![]()
![]()
![]()
Note: A geodesic equation applies to electromagnetism!
Normalize and study perturbations:
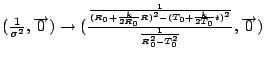
Take the derivative with respect to ![]() and
and ![]() .
.
![]()
![]()
Plug into the force of gravity proposal, assuming the Christoffel symbol is zero which will be the case for a weak field in Euclidean coordinates. Note the contravariant derivative flips a sign.
![]()
fbox
![]()
Must break spacetime symmetry.
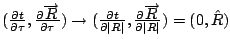

![]()
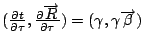
Lightlike events in Newtonian spacetime.
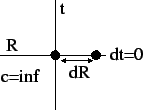
![]()
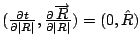
![]()
The force equation is two second order differential equations (assuming radial symmetry) [sigma squared equals minus tau squared].
![]()
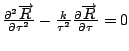
Substitute
 to create first order equations.
to create first order equations.
![]()
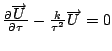
Solve.
![]()
For flat spacetime,
![]() The constraint on relativistic velocities in flat spacetime is:
The constraint on relativistic velocities in flat spacetime is:
![]()
Solve for the constants, and plug back into the constraint,
multiplying through by ![]()
![]()
![]()
Taylor series expansion to second order in
![]()
fbox
![]()
Apply the chain rule to the force equation.
![]()
Assume:
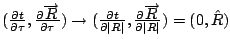
![]()
Both the three-vectors are constants, creating a first order differential equation.
![]()
Solve.
![]()
![]()
For thin disk galaxies
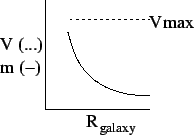
After reaching ![]() has a constant velocity while the mass decays exponentially. It might
match this equation, but needs to be looked at in detail.
has a constant velocity while the mass decays exponentially. It might
match this equation, but needs to be looked at in detail.
For the early Universe:
The very high density of the early Universe combined with its uniform velocity distribution would be consistent with the constant velocity solution of the gravitational force equation dominating the dynamics. The solution is stable.
Using a nineteenth century approach, two pillars of twentieth century physics have been fused, general relativity and the standard model. Both required technical modifications. The description of geodesics by general relativity is not complete because it does not explicitly show how the potential source causes curvature. A dynamic metric equation is found but it uses a simpler set of field equations (a rank 1 tensor instead of 2). In the standard model as elsewhere, combining two 4-vectors requires a metric. By normalizing the 4-vectors, the unitary aspect of the standard model can be self-evident. Although not mentioned before, the normalization process is essential to getting the dimensional analysis right.
This theory makes three testable predictions, two subtle, one not.
First, the polarity of gravitational waves will be scalar or longitudinal,
not transverse as predicted by general relativity. Second, if gravitation
effects are measured to secondary post Newtonian accuracy, the coefficients
for the metric derived here are different from the Schwarzschild metric
in isotropic coordinates. Such an experiment will be quite difficult
to do. The third test is to see if the complete relativistic force
equation matches all the data for a thin spiral galaxy. It is this
test which should be investigated first.