Quantization

The classical electromagnetic Lagrangian cannot be quantized. One way to realize this is to calculate the canonical conjugate of the fields, the generalized 4-momentum:

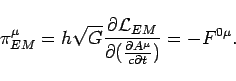$$\pi_{EM}^{\mu}=h\sqrt{G}\frac{\partial\mathcal{L}_{EM}}{\partial(\frac{\partial A^{\mu}}{c\partial t})}=-F^{0\mu}.$$ (34)

Unfortunately, the energy component of the momentum operator is zero. The commutator of the complementary variables of the potential and energy, $[A^{0},\pi^{0}]$, will equal zero, and cannot be quantized. The momentum for the GEM Lagrangian does not suffer from this problem:

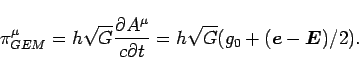$$\pi_{GEM}^{\mu}=h\sqrt{G}\frac{\partial A^{\mu}}{c\partial t}=h\sqrt{G}(g_{0}+(\bi{e}-\bi{E})/2).$$ (35)

When expressed with operators, the commutator $[A^{0},\pi^{0}]$ will not be zero, so the field may be quantized. If the gravitational fields are zero, the generalized 4-momentum is the same as for standard electromagnetic field theory, thus passing another consistency check. The field equations (5) are similar to the classical electromagnetic Lagrangian with the choice of the Lorenz gauge, the difference being an additional mass current density source. Gupta and Bleuler have quantized the modes of radiation for a four dimensional wave equation.[1,3] They determined that there were four modes of transmission: two transverse, one scalar, and one longitudinal mode. The scalar polarization mode represents a significant technical problem since its norm may be negative. They introduce a supplemental condition to ensure the scalar and longitudinal modes are virtual.

The field in the GEM model must represent both gravity and electromagnetism. The two transverse modes are spin-1 photons that do all the work of electromagnetism. The symmetric second-rank field strength tensor cannot be represented by a photon because photons transform differently than a symmetric tensor. For a long-range force where like charges attract, the spin must be an even integer. Whatever particle does the work must travel at the speed of light like the transverse modes. Since the symmetric tensor is rank two, that can be represented by a spin-2 graviton.

The scalar field formed from the trace of the asymmetric GEM field strength tensor may be able to play a role similar to the scalar Higgs field. Since the scalar field is entirely a function of the gravity field $g^{\mu}$, the symmetry of the electromagnetic field is not affected. That is a key requirement for any mechanism to introduce mass into the standard model. For the graviton, the trace of the asymmetric tensor must be equal to zero so that the graviton travels at the speed of light. Particles with mass and with or without electric charge will have a non-zero trace.

There are efforts underway to detect the transverse gravitational waves predicted by general relativity. This model predicts the polarization of a gravitational wave will be either scalar or longitudinal, with the transverse modes reserved for light. The detection of the first gravitational wave polarization will mark either success or failure of the GEM field theory.