Classical gravitational force and a new effect

Minkowski spacetime is different from Newtonian space and time due to the way one measures distance, four dimensional versus three. Spacetime symmetry must be broken. The Minkowski interval $\tau$ is a consequence of the relationship between time $t$ and space $\bi{R}$. For classical physics, the functional relationship between time and space must be severed. In the static field approximation, there is a scalar distance $R$ which is the same magnitude as the interval $\tau$. If the interval $\tau$ is replaced by the scalar distance $R$ in the relativistic 4-velocity, then that will sever the functional relationship between time and space:

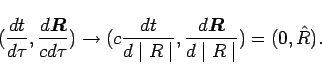$$(\frac{dt}{d\tau},\frac{d\bi{R}}{cd\tau})\rightarrow(c\frac{dt}{d\mid R\mid},\frac{d\bi{R}}{d\mid R\mid})=(0,\hat{R}).$$ (30)

Substitute into weak-field gravitational Lorentz 4-force density equation (23) to create a classical 3-force equation:

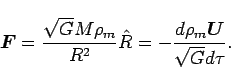$$\bi{F}=\frac{\sqrt{G}M\rho_{m}}{R^{2}}\hat{R}=-\frac{d\rho_{m}\bi{U}}{\sqrt{G}d\tau}.$$ (31)

This is not quite Newton's gravitational force density law. The reason is that one must now consider the right-hand side of the force equation carefully. According to the chain rule:

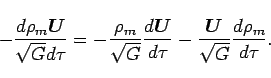$$-\frac{d\rho_{m}\bi{U}}{\sqrt{G}d\tau}=-\frac{\rho_{m}}{\sqr... ...d\bi{U}}{d\tau}-\frac{\bi{U}}{\sqrt{G}}\frac{d\rho_{m}}{d\tau}.$$ (32)

An open question is how should spacetime symmetry be broken for the derivatives with respect to the interval $\tau$? An interval is composed of both changes in time and space. For the acceleration term, $\frac{\partial\bi{\bi{U}}}{\partial\tau}$, if the interval is only about time, then one gets back Newtonian acceleration, a second derivative of time. One might be tempted to use time in the mass distribution in spacetime term, $\frac{\partial\rho_{m}}{\partial\tau}$. However, the system is presumed to be static, so this would be zero by presumption. If this derivative is to have any chance at being non-zero, it would have to change with respect to the scalar distance $R$ as has been done earlier in the derivation. Note that this new term will not point in a radial direction. Instead, the change in mass with respect to space points in the direction of the velocity of that mass. The classical 3-force law would look like so:

$$\frac{\sqrt{G}M\rho_{m}}{R^{2}}(\hat{R}+\hat{V})=-\frac{\rho... ...^{2}}-\frac{c\bi{V}}{\sqrt{G}} \frac{d\rho_{m}}{d\mid R\mid}.$$ (33)

For a point source, the change in mass distribution term, $d\rho_{m}/d\mid R\mid$, will not make a contribution, and one gets Newton's law of gravity. It is only if the inertial mass is distributed over space as is the case for galaxies will the new effect term come into play. If the velocity is constant, then the acceleration is zero. The equation describes the distribution in space of the inertial mass density $\rho_{m}$ that contributes to the total gravitational source mass $M$. The solution to 33 when there is no acceleration has the inertial mass distribution that decays exponentially. There is a problem with the rotation profile of thin disk galaxies.[7,8] Once the maximum velocity is reached, the velocity stays constant while the mass density declines exponentially. It has been shown that galaxies should not be stable at all.[14] The new effect term promises a stable exponential decay of the mass distribution for large radii with constant velocity, which sounds like a fit. The new effect has an inverse distance dependence for small accelerations due to the factor of c required to get the units right, which matches the MOND proposal that has been successfully applied to explain the velocity profile of thin disk galaxies.[10]