Lagrange densities

The classic electromagnetic Lagrange density has two terms: one for electric charge density coupling to the potential and another for the antisymmetric second-rank field strength tensor $F^{\mu\nu}$:

$$\mathcal{L}_{EM}=-\frac{1}{c}J_{q}^{\mu}A_{\mu}-\frac{1}{4c^... ...al^{\nu}A^{\mu})(\partial_{\mu}A_{\nu}-\partial_{\nu}A_{\mu}).$$ (1)

An analogous Lagrangian for gravity should contain these components, but changes are required. Gravity would couple the potential to the mass current density, not the electric current density or a second-rank energy density tensor. Mass does not have the same units as electric charge, so mass will have to be multiplied by the square root of Newton's gravitational constant $G$ to keep the units identical. Where there is a negative electric current density, a positive mass current density will be substituted. A change in sign is required so that like mass currents attract for gravity. Because gravity effects metrics which are symmetric, the field strength tensor for gravity must also be symmetric. In order that the symmetric object transforms like a tensor, the exterior derivative must be replaced by a covariant derivative:

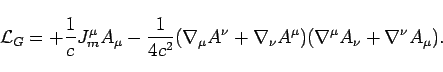$$\mathcal{\mathcal{L}}_{G}=+\frac{1}{c}J_{m}^{\mu}A_{\mu}-\fr... ...+\nabla_{\nu}A^{\mu})(\nabla^{\mu}A_{\nu}+\nabla^{\nu}A_{\mu}).$$ (2)

A mixed derivative is used for the field strength tensor so that a scalar field can be defined by taking the trace. The trace will be zero for massless particles like a graviton or photon, but nonzero for massive particles. The unified Lagrangian will be the sum of these two, $\mathcal{L}_{EM}$ and $\mathcal{L}_{G}$, which separately only apply if the other charge is zero and the corresponding vacuum field strength tensor is zero. Without loss of generality, the exterior derivatives in the electromagnetic Lagrangian (1) can be written as covariant derivatives. This leads to the gravity and electromagnetism (GEM) Lagrangian:

$$\mathcal{\mathcal{L}}_{GEM}=-\frac{1}{c}(J_{q}^{\mu}-J_{m}^{... ..._{\mu}-\frac{1}{2c^{2}}\nabla_{\mu}A^{\nu}\nabla^{\mu}A_{\nu}.$$ (3)

The Fermi Lagrangian of electromagnetism is a subset of 3. This establishes a link to electromagnetism. A covariant derivative contains the connection. For a metric compatible, torsion-free connection, the Christoffel symbol is a function of derivatives of the metric. As such, the derivatives of the metric may be constrained by the GEM Lagrangian, unlike the case with the exterior derivative of the classical electromagnetic Lagrangian. The possibility to do both gravity and electromagnetism is here.

With the Hilbert action of general relativity, one considers the second-rank metric tensor to be a field. By varying the metric, non-linear second-rank field equations result that dictate how the metric changes. In the GEM Lagrangian, a dynamic metric is possible due to a diffeomorphism symmetry in the Lagrangian introduced when changing from an exterior derivative used in the electromagnetic field strength tensor to a covariant derivative in the unified field strength tensor. Any change in the unified field strength tensor could be due to a change in the potential, or due to a change in the metric via the connection. One can choose a metric as the gauge, and then calculate the potential for a given field strength tensor, or choose a fix the potential, and calculate the appropriate connection.