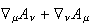 )/2
for gravity just as an antisymmetric
(
)/2
for gravity just as an antisymmetric
(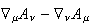 )/2
tensor is used for EM. Here are the 5 fields that play a central role in this
proposal:
)/2
tensor is used for EM. Here are the 5 fields that play a central role in this
proposal:
Douglas B. Sweetser
sweetser@alum.mit.edu
This proposal represents a variation on the Maxwell equations for EM. In
fact, the Maxwell equations are a formal subset of the GEM field equations.
The core idea is to use a symmetric tensor
(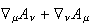 )/2
for gravity just as an antisymmetric
(
)/2
for gravity just as an antisymmetric
(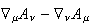 )/2
tensor is used for EM. Here are the 5 fields that play a central role in this
proposal:
)/2
tensor is used for EM. Here are the 5 fields that play a central role in this
proposal:
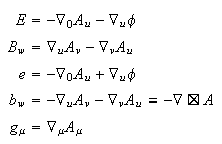
Together these compose all the terms in the manifestly covariant tensor
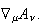 Instead
of using tensors, I will be using quaternions, a 4-dimensional division
algebra. Because it is a division algebra, an inverse of any field equation
necessarily exists, something needed by quantum field theory to determine the
propagator.
Instead
of using tensors, I will be using quaternions, a 4-dimensional division
algebra. Because it is a division algebra, an inverse of any field equation
necessarily exists, something needed by quantum field theory to determine the
propagator.
The Lagrangian of EM is the difference between the square of the B field and the square of the E field. A quaternion differential acting on a quaternion potential generates three of the five fields:
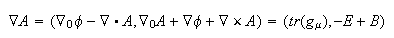
The scalar has all the terms that make up a typical gauge for EM. The scalar is easily eliminated by subtracting the conjugate:
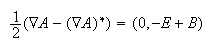
In this early stage, one can see that a proposal built from these quaternion
operators will be invariant under a gauge transformation since the
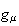 field has already been subtracted away (usually one looks for the symmetry of
the field equations, derived later).
field has already been subtracted away (usually one looks for the symmetry of
the field equations, derived later).
By changing the order of the differential and the potential, the sign of B is changed. Use this trick to get the difference of the two fields:
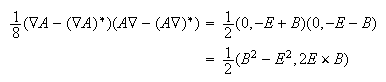
Notice the 3-vector is the Poynting vector, vital for conservation laws in EM. The Lagrangian uses only the scalar which can be isolated by adding the conjugate of this expression.
Write out the Lagrangian in terms of its components, including the current coupling term:
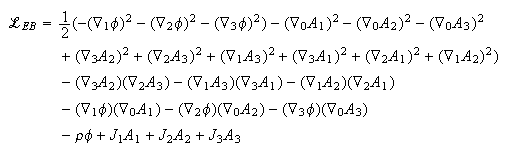
Calculate the field equations using the Euler-Lagrange equations, taking the derivatives of the Lagrangian with respect to the potential and the derivatives of the potential:
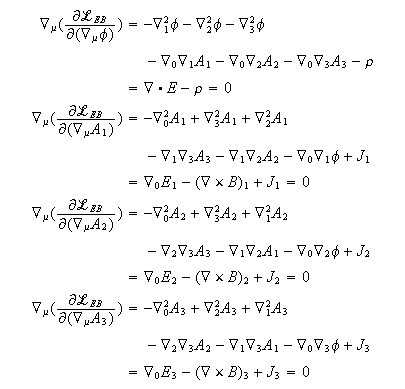
These results can be summarized with the Maxwell source field equations:
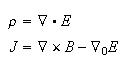
The only part of this derivation that was non-standard occurred early with the use of quaternions operators to generate the Lagrangian in eq. LEB generator. From there onward, the covariant notation and calculation may be more detailed than one normally sees, but the math is the same. This exercise was done so the small variations for the gravity proposal may be more easily spotted against this background of the most successful field theory in physics.
A riddle: how can one represent the symmetric
 field using quaternions? A key word in the riddle references representation
theory. What is needed is a representation of quaternions that has a
symmetric curl. The standard Hamilton 4x4 real matrix representation of a
quaternion looks like this:
field using quaternions? A key word in the riddle references representation
theory. What is needed is a representation of quaternions that has a
symmetric curl. The standard Hamilton 4x4 real matrix representation of a
quaternion looks like this:
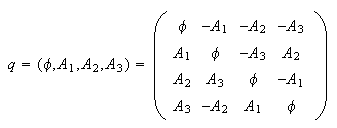
To make sure no signs flip, make all the terms positive, what I will call the "Even representation" of quaternions (also known as the hypercomplex numbers developed by Clyde Daven):
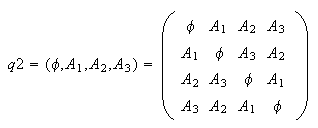
While this 4x4 real matrix will create a symmetric curl, it raises a new
puzzle: how does one guarantee this is a division algebra? The answer is to
exclude the eigenvalues from the possible values of
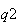 ,
and then an inverse will necessarily exist. Given the important role of
eigenvalues in quantum mechanics, this is an interesting constraint whose
implications I do not fully understand.
,
and then an inverse will necessarily exist. Given the important role of
eigenvalues in quantum mechanics, this is an interesting constraint whose
implications I do not fully understand.
The Lagrangian of gravity is the difference between the square of the symmetric b field and the square of the e field. The order of the differential operator and potential does not matter for the Even representation. The conjugate operator can be used to generate the fields needed for gravity:
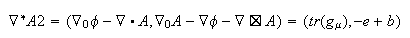
Again the scalar has all the terms that make up a typical gauge. Eliminate by subtracting the conjugate:
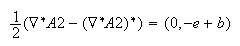
Again a gauge-invariant field theory is promised.
By changing the order of conjugation, the sign of the
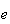 field is changed. Use this trick to get the difference of the two fields:
field is changed. Use this trick to get the difference of the two fields:
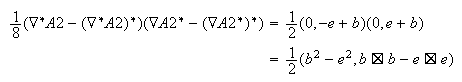
The meaning of the 3-vector is unclear at this time. The Lagrangian uses only the scalar which can be isolated by adding the conjugate of this expression.
Write out the Lagrangian for gravity in terms of its components, including the current coupling term:
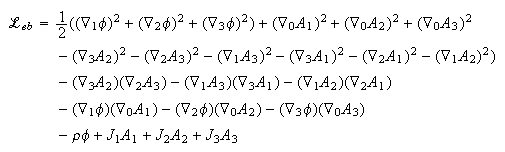
What has changed are the signs of all the pure terms, while all the mixed terms keep their signs.
Calculate the field equations using the Euler-Lagrange equations, taking the derivatives of the Lagrangian with respect to the potential and the derivatives of the potential:
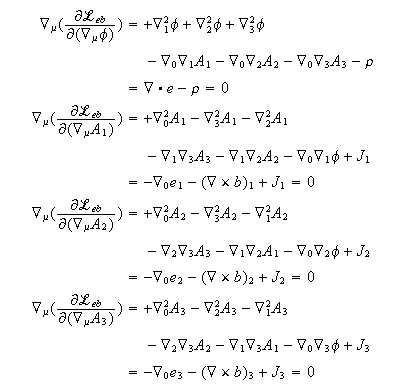
These results can be summarized with the symmetric field Maxwell source field equations:
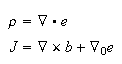
One can spot a manifestly covariant form of Newton's law of gravity in eq.
Newton's law. The static form of Newton's law is
there. If the mass density changes, there is a time derivative of
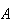 that can respond in a way consistent with special relativity. Like charges
attract because when the charge density is put on the other side of the
equality, they have the same sign. Like charges repel for Gauss' static force
law, eq. Euler-Lagrange: Gauss, because the signs are
opposite.
that can respond in a way consistent with special relativity. Like charges
attract because when the charge density is put on the other side of the
equality, they have the same sign. Like charges repel for Gauss' static force
law, eq. Euler-Lagrange: Gauss, because the signs are
opposite.
Tests of the equivalence principle have proven that one must have a dynamic metric solution for gravity. People accustom to general relativity expect a gravity proposal to be exclusively about geometry. What the GEM proposal does is the ultimate compromise between a potential and metric theory: there is a choice whether to account for gravity as a potential or metric theory or a combination of both. The symmetry can be seen in the definition of a covariant derivative:
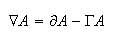
A covariant derivative is the difference between the change in the potential, and the connection, which is changes in the metric. With a flat, Minkowski metric in Euclidean coordinates, the connection will be zero everywhere, so the covariant derivative is identical with the standard derivative. One could choose to work with a potential that was constant, in which case all the variation found in the covariant derivative comes from the connection. In this case, if one forms the field equations, one takes a derivative of the covariant derivative, which in turn means one forms a second-order differential equation for the metric. By solving the second order differential equation, one can determine what the metric is for a physical situation. This I will now do.
Start with relativistic Newtonian law of gravity, eq. Newton's law, under the assumptions that the system is static, spherically symmetric, uncharged, with a constant potential:
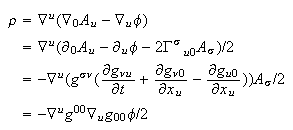
A metric consistent with weak field tests must be found that satisfies this differential equation. It is known as the Rosen metric, although I prefer to call it the exponential metric, since the name is more descriptive:
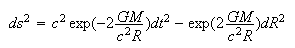
When one takes the derivative of the
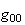 term, one gets an exponential back, which neatly cancels the exponential in
term, one gets an exponential back, which neatly cancels the exponential in
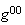 .
One ends up with the Laplacian operator acting on a charge/R potential, which
should sound familiar.
.
One ends up with the Laplacian operator acting on a charge/R potential, which
should sound familiar.
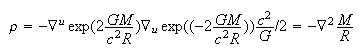
The metric solution looks like a potential solution. This is a mathematical demonstration of similarities for a potential and metric explanation of gravity.
The technical problem with Rosen's work is that is posits a fixed background metric. This structure can store energy and momentum, so that dipole emissions of gravity waves are possible. Yet the rate of gravity wave energy emission is consistent with a quadrapole being the lowest mode of emission. A common problem for theories that add another component to general relativity is the dipole mode of emission becomes possible. The GEM proposal is actually simpler than general relativity in the following way. The Riemann curvature tensor contains the difference of two derivatives of connections. This is where the second order derivatives of the metric reside. The GEM equation only contains one second order derivative of a metric, and is thus simpler than general relativity.
Like charges attract for gravity, while they repel for EM. This requires the
particles have spin 2 and spin 1 respectively. The symmetry of the mediating
particles can be seen in two places. First there are the two field strength
tensors, the symmetric rank 2 tensor
(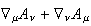 )/2
for gravity and the antisymmetric rank 2 tensor
(
)/2
for gravity and the antisymmetric rank 2 tensor
(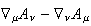 )/2
for EM. These make respective homes for the graviton and the photon.
)/2
for EM. These make respective homes for the graviton and the photon.
The second place to see the mediating particle symmetry is in the current
coupling term. One usually takes the Fourier transform of the potential, and
looks at the current-current interaction. Here the phases of the two tell use
what kind of particle can participate in the interaction. If the phase takes
2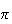 to get back to the start, then the system has spin 1 symmetry. If it only
takes
to get back to the start, then the system has spin 1 symmetry. If it only
takes
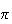 radians, the phase has spin 2 symmetry.
radians, the phase has spin 2 symmetry.
The scalar has already been written down as part of the Lagrangian as a Lorentz invariant contraction of two four vectors. There are two ways to reproduce the contractions using the Hamilton and Even representations of quaternions:
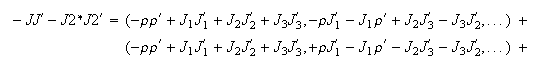
If the two currents happen to be pointing in nearly the same direction, there
are contributions to both a spin 1 and spin 2 symmetry for all the terms that
are part of the phase. Those pairs that have the same sign are part of spin 2
symmetry because they effectively work together to get around twice as fast.
When the two have opposite signs, it will require the normal
2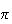 ,
so it is spin 1 symmetry. The phase of the current-current interaction
requires a unified field theory.
,
so it is spin 1 symmetry. The phase of the current-current interaction
requires a unified field theory.